解题思路 or 实现原理

在计算机科学中, 二叉树是每个节点最多只有两个分支的树结构。通常分支被称作 "左子树" 或 "右子树"。二叉树的分支具有左右次序, 不能随意颠倒。

二叉树的性质

• 二叉树的第i层至多有 $2^{i-1}$ 个结点;

• 深度为k的二叉树至多有 $2^{i-1}$ 个结点;

• 包含n个结点的二叉树的高度至少为 $log_2(n + 1)$;

• 对任何一颗 二叉树T, 如果其终端结点数为$n_0$, 度为 2 的结点数为$n_2$, 则 $n_0 = n_2 + 1$

特殊类型

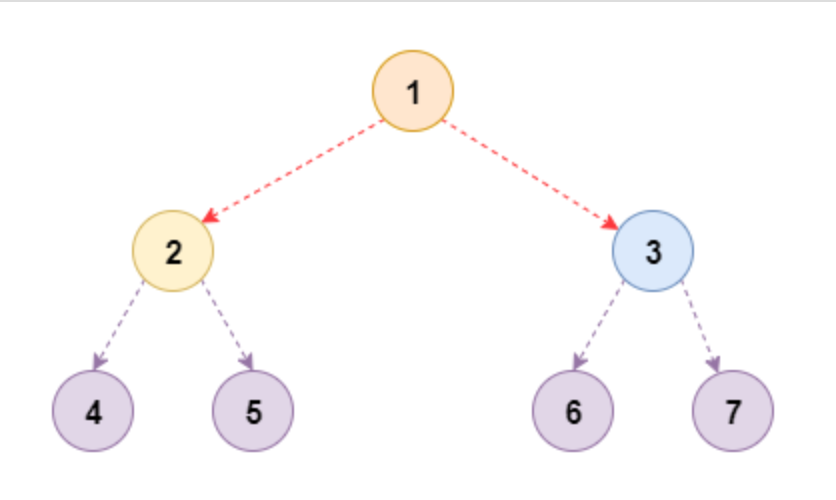
满二叉树

• 定义: 除最后一层结点均无任何子节点外, 每一层的所有结点都有两个子结点的树

• 性质:

  • 一棵树的深度为 h, 最大层数为 k, 深度与最大层数相同, k=h;
  • 叶子数为 $2^h$;
  • 第 k 层的结点数是: $2^{k-1}$;
  • 总结点数是 $2^k-1$, 且总节点数一定是奇数。

完全二叉树

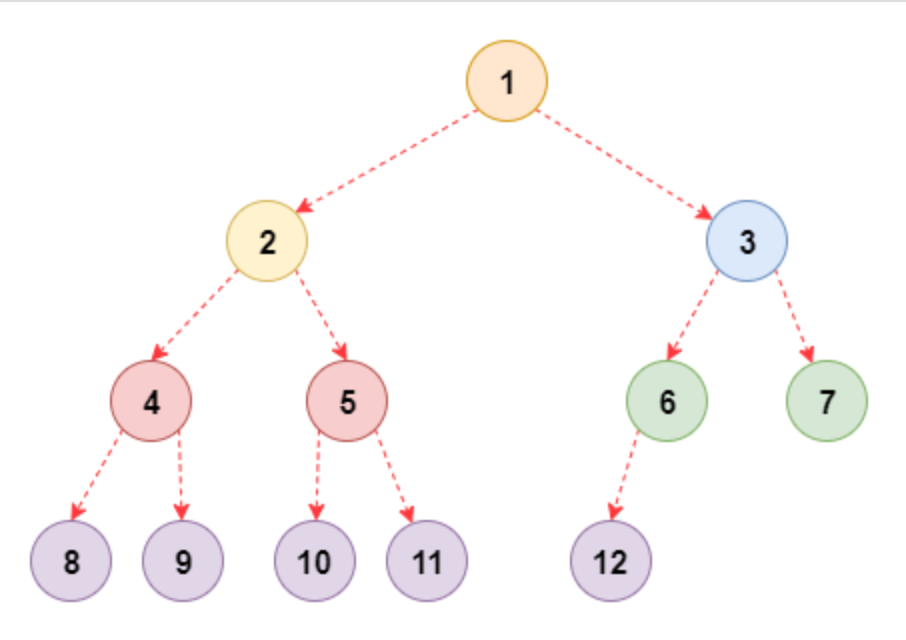
• 定义: 一颗二叉树中, 只有最小面两层结点的度可以小于2, 并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为 完全二叉树。

• 特点: 叶子结点只能出现在最下层和次下层, 且最小层的叶子结点集中在树的左部。显然, 一颗满二叉树必定是一颗完全二叉树, 而完全二叉树未必是满二叉树。

• Note: 完全二叉树 是效率很高的数据结构, 堆是一种完全二叉树或者近似完全二叉树, 所以效率极高, 像十分常用的排序算法、Dijkstra 算法、Prim 算法等都要用堆才能优化, 二叉排序树的效率也要借助平衡树来提高, 而平衡性基于完全二叉树。

实现代码

/*
 * @Author: Rainy
 * @Date: 2019-11-14 19:25:01
 * @LastEditors  : Rainy
 * @LastEditTime : 2020-02-04 17:10:36
 */

import { WithParamsFunction } from 'types';

type TreeReturn = BinaryTree | null;

export class BinaryTree {
  key: any;
  left: any = null;
  right: any = null;
  root: any = null;

  constructor(key: any) {
    this.key = key;
    this.left = null;
    this.right = null;
  }

  _insertNode(node: BinaryTree, newNode: BinaryTree): void {
    if (node.key > newNode.key) {
      if (node.left) {
        this._insertNode(node.left, newNode);
      } else {
        node.left = newNode;
      }
    } else {
      if (node.right) {
        this._insertNode(node.right, newNode);
      } else {
        node.right = newNode;
      }
    }
  }
  insert(key: any) {
    let newNode = new BinaryTree(key);
    if (this.root) {
      this._insertNode(this.root, newNode);
    } else {
      this.root = newNode;
    }
  }

  _searchNode(node: BinaryTree, key: any): boolean {
    if (!node) {
      return false;
    }
    if (node.key > key) {
      this._searchNode(node.left, key);
    } else if (node.key < key) {
      this._searchNode(node.right, key);
    } else {
      return true;
    }
    return false;
  }
  search(node: BinaryTree, key: any): any {
    this._searchNode(this.root, key);
  }

  _findMinNode(node: BinaryTree): TreeReturn {
    if (node) {
      while (node && node.left) {
        node = node.left;
      }
      return node;
    }
    return null;
  }
  _minNode(node: BinaryTree): BinaryTree | any {}
  min(): any {}

  _findMaxNode(node: BinaryTree): TreeReturn {
    return null;
  }
  _maxNode(node: BinaryTree): BinaryTree | any {}
  max(): any {}

  _removeNode(node: BinaryTree, key: any): TreeReturn {
    if (node === null) {
      return null;
    }
    if (node.key > key) {
      node.left = this._removeNode(node.left, key);
    } else if (node.key < key) {
      node.right = this._removeNode(node.right, key);
    } else {
      if (node.left === null && node.right === null) {
        // @ts-ignore
        node = null;
      }
      if (node.left === null) {
        node = node.right;
      }
      if (node.right === null) {
        node = node.left;
      }

      let aux: { key: any } | null = this._findMinNode(node.right);
      if (aux) {
        node.key = aux.key;
        node.right = this._removeNode(node.right, aux.key);
      }
    }
    return node;
  }
  remove(key: any) {
    this.root = this._removeNode(this.root, key);
  }

  _preOrderTraverseNode(
    node: BinaryTree,
    callback: WithParamsFunction | any
  ): void {
    if (node) {
      callback & callback(node.key);
      this._preOrderTraverseNode(node.left, callback);
      this._preOrderTraverseNode(node.right, callback);
    }
  }

  preOrderTraverse(callback: WithParamsFunction | any): void {
    this._preOrderTraverseNode(this.root, callback);
  }

  _inOrderTraverseNode(
    node: BinaryTree,
    callback: WithParamsFunction | any
  ): void {
    if (node) {
      this._inOrderTraverseNode(node.left, callback);
      callback & callback(node.key);
      this._inOrderTraverseNode(node.right, callback);
    }
  }
  inOrderTraverse(callback: WithParamsFunction | any): void {
    this._inOrderTraverseNode(this.root, callback);
  }

  _postOrderTraverseNode(
    node: BinaryTree,
    callback: WithParamsFunction | any
  ): void {
    if (node) {
      this._postOrderTraverseNode(node.left, callback);
      this._postOrderTraverseNode(node.right, callback);
      callback & callback(node.key);
    }
  }
  postOrderTraverse(callback: WithParamsFunction | any): void {
    this._postOrderTraverseNode(this.root, callback);
  }
}

参考资料

二叉树 (opens new window)

满二叉树 (opens new window)

完全二叉树 (opens new window)